Правило нули функции. Нуль функции Как находить нули функции по уравнению

2. Найдем нули функции.

f(x) при х .

Ответ f(x) при х .

2) х 2 >-4x-5;

x 2 +4x +5>0;

Пусть f(x)=х 2 +4х +5 тогда Найдем такие х при которых f(x)>0,

D=-4 Нет нулей.

4. Системы неравенств. Неравенства и системы неравенств с двумя переменными

1) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств.

2) Множество решений неравенства f(х;у)>0 можно графически изобразить на координатной плоскости. Обычно линия, заданная уравнением f(х;у)=0 ,разбивает плоскость на 2 части, одна из которых является решением неравенства. Чтобы определить, какая из частей, надо подставить координаты произвольной точки М(х0;у0) , не лежащей на линии f(х;у)=0, в неравенство. Если f(х0;у0) > 0 , то решением неравенства является часть плоскости, содержащая точку М0. если f(х0;у0)<0, то другая часть плоскости.

3) Множество решений системы неравенств есть пересечение множеств решений входящих в нее неравенств. Пусть, например, задана система неравенств:

.

Для первого неравенства множество решений есть круг радиусом 2 и с центром в начале координат, а для второго- полуплоскость, расположенная над прямой 2х+3у=0. Множеством решений данной системы служит пересечение указанных множеств, т.е. полукруг.

4) Пример. Решить систему неравенств:

Решением 1-го неравенства служит множество , 2-го множество (2;7) и третьего - множество .

Пересечением указанных множеств является промежуток(2;3], который и есть множество решений системы неравенств.

5. Решение рациональных неравенств методом интервалов

В основе метода интервалов лежит следующее свойство двучлена (х-а): точка х=α делит числовую ось на две части - справа от точки α двучлен (х‑α)>0, а слева от точки α (х-α)<0.

Пусть требуется решить неравенство (x-α 1)(x-α 2)...(x-α n)>0, где α 1 , α 2 ...α n-1 , α n - фиксированные числа, среди которых нет равных, причем такие, что α 1 < α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 методом интервалов поступают следующим образом: на числовую ось наносят числа α 1 , α 2 ...α n-1 , α n ; в промежутке справа от наибольшего из них, т.е. числа α n , ставят знак «плюс», в следующем за ним справа налево интервале ставят знак «минус», затем - знак «плюс», затем знак «минус» и т.д. Тогда множество всех решений неравенства (x-α 1)(x‑α 2)...(x-α n)>0 будет объединение всех промежутков, в которых поставлен знак «плюс», а множество решений неравенства (x-α 1)(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Решение рациональных неравенств (т.е неравенств вида P(x) Q(x) где – многочлены) основано на следующем свойстве непрерывной функции: если непрерывная функция обращается в нуль в точках х1 и х2 (х1;х2) и между этими точками не имеет других корней, то в промежутках(х1;х2) функция сохраняет свой знак.

Поэтому для нахождения промежутков знакопостоянства функции y=f(x) на числовой прямой отмечают все точки, в которых функция f(x) обращается в нуль или терпит разрыв. Эти точки разбивают числовую прямую на несколько промежутков, внутри каждого из которых функция f(x) непрерывна и не обращается в нуль, т.е. сохраняет знак. Чтобы определить этот знак, достаточно найти знак функции в какой либо точке рассматриваемого промежутка числовой прямой.

2) Для определения интервалов знакопостоянства рациональной функции, т.е. Для решения рационального неравенства, отмечаем на числовой прямой корни числителя и корни знаменателя, которые как и являются корнями и точками разрыва рациональной функции.

Решение неравенств методом интервалов

3. < 20.

Решение. Область допустимых значений определяется системой неравенств:

Для функции f(x) = – 20. Находим f(x):

откуда x = 29 и x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10 < 0.

Ответ: . Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений - приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по...

X изменяется на промежутке (0,1], и убывает на промежутке .

Мы видим, что добавление n к аргументу x , не меняет

значение функции. Наименьшее отличное от нуля число

из n есть , таким образом, это период sin 2 x .

Нули функции. Значение аргумента, при котором функция равна 0, называется нулём ( корнем) функции . Функция может иметь несколько нулей. Например, функция y = x (x + 1) (x — 3) имеет три нуля: x = 0, x = — 1, x = 3. Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х .

На рис.7 представлен график функции с нулями: x = a , x = b и x = c .

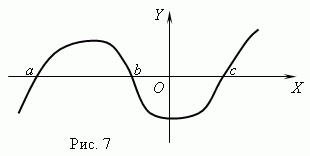
Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой .

Тема 6. «Метод интервалов».

Если f (x) f (x 0) при х х 0 , то функцию f (x) называют непрерывной в точке х 0 .

Если функция непрерывна в каждой точке некоторого промежутка I , то ее называют непрерывной на промежутке I (промежуток I называют промежутком непрерывности функции ). График функции на этом промежутке представляет собой непрерывную линию, о которой говорят, что ее можно «нарисовать, не отрывая карандаша от бумаги».

Свойство непрерывных функций.

Если на интервале (a ; b) функция f непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак.

На этом свойстве основан метод решения неравенств с одной переменной – метод интервалов. Пусть функция f(x) непрерывна на интервале I и обращается в нуль в конечном числе точек этого интервала. По свойству непрерывных функций этими точками I разбивается на интервалы, в каждом из которых непрерывная функция f(x) c охраняет постоянный знак. Чтобы определить этот знак, достаточно вычислить значение функции f(x) в какой-либо одной точке из каждого такого интервала. Исходя из этого, получим следующий алгоритм решения неравенств методом интервалов.

Метод интервалов для неравенств вида

Метод интервалов. Средний уровень.

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Линейная функция

Линейной называется функция вида. Рассмотрим для примера функцию. Она положительна при 3″> и отрицательна при. Точка – нуль функции (). Покажем знаки этой функции на числовой оси:

Говорим, что «функция меняет знак при переходе через точку ».

Видно, что знаки функции соответствуют положению графика функции: если график выше оси, знак « », если ниже – « ».

Если обобщить полученное правило на произвольную линейную функцию, получим такой алгоритм:

Квадратичная функция

Надеюсь, ты помнишь, как решаются квадратные неравенства? Если нет, прочти тему «Квадратные неравенства». Напомню общий вид квадратичной функции: .

Теперь вспомним, какие знаки принимает квадратичная функция. Ее график – парабола, и функция принимает знак « » при таких, при которых парабола выше оси, и « » – если парабола ниже оси:

Если у функции есть нули (значения, при которых), парабола пересекает ось в двух точках – корнях соответствующего квадратного уравнения. Таким образом ось разбивается на три интервала, а знаки функции попеременно меняются при переходе через каждый корень.

А можно ли как-нибудь определить знаки, не рисуя каждый раз параболу?

Вспомним, что квадратный трехчлен можно разложить на множители:

Отметим корни на оси:

Мы помним, что знак функции может меняться только при переходе через корень. Используем этот факт: для каждого из трех интервалов, на которые ось разбивается корнями, достаточно определить знак функции только в одной произвольно выбранной точке: в остальных точках интервала знак будет таким же.

В нашем примере: при 3″> оба выражения в скобках положительны (подставим, например: 0″>). Ставим на оси знак « »:

Ну и, при (подставь, например,) обе скобки отрицательны, значит, произведение положительно:

Это и есть метод интервалов : зная знаки сомножителей на каждом интервале, определяем знак всего произведения.

Рассмотрим также случаи, когда нулей у функции нет, или он всего один.

Если их нет, то и корней нет. А значит, не будет и «перехода через корень». А значит, функция на всей числовой оси принимает только один знак. Его легко определить, подставив в функцию.

Если корень только один, парабола касается оси, поэтому знак функции не меняется при переходе через корень. Какое правило придумаем для таких ситуаций?

Если разложить такую функцию на множители, получатся два одинаковых множителя:

А любое выражение в квадрате неотрицательно! Поэтому знак функции и не меняется. В таких случаях будем выделять корень, при переходе через который знак не меняется, обведя его квадратиком:

Такой корень будем называть кратным .

Метод интервалов в неравенствах

Теперь любое квадратное неравенство можно решать без рисования параболы. Достаточно только расставить на оси знаки квадратичной функции, и выбрать интервалы в зависимости от знака неравенства. Например:

Отмерим корни на оси и расставим знаки:

Нам нужна часть оси со знаком « »; так как неравенство нестрогое, сами корни тоже включаются в решение:

Теперь рассмотрим рациональное неравенство – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).

Пример:

Все множители кроме одного – – здесь «линейные», то есть, содержат переменную только в первой степени. Такие линейные множители нам и нужны для применения метода интервалов – знак при переходе через их корни меняется. А вот множитель вообще не имеет корней. Это значит, что он всегда положительный (проверь это сам), и поэтому не влияет на знак всего неравенства. Значит, на него можно поделить левую и правую часть неравенства, и таким образом избавиться от него:

Теперь все так же, как было с квадратными неравенствами: определяем, в каких точках каждый из множителей обращается в нуль, отмечаем эти точки на оси и расставляем знаки. Обращаю внимание очень важный факт:

В случае четного количества поступаем так же, как и раньше: обводим точку квадратиком и не меняем знак при переходе через корень. А вот в случае нечетного количества это правило не выполняется: знак все-равно поменяется при переходе через корень. Поэтому с таким корнем ничего дополнительно не делаем, как будто он у нас не кратный. Вышеописанные правила относятся ко всем четным и нечетным степеням.

Что запишем в ответе?

При нарушении чередования знаков нужно быть очень внимательным, ведь при нестрогом неравенстве в ответ должны войти все закрашенные точки . Но некоторые из нах часто стоят особняком, то есть не входят в закрашенную область. В этом случае мы добавляем их к ответу как изолированные точки (в фигурных скобках):

Примеры (реши сам):

Ответы:

1. Если среди множителей просто – это корень, ведь его можно представить как.
   .

Что такое нули функции? Ответит довольно прост - это математический термин, под которым подразумевают область определения заданной функции, на котором ее значение нулевое. Нули функции также называют Проще всего пояснить, что такое нули функции, на нескольких простых примерах.

Примеры

Рассмотрим несложное уравнение у=х+3. Поскольку нуль функции - это значение аргумента, при котором у приобрел нулевое значение, подставим 0 в левую часть уравнения:

В данном случае -3 и есть искомый нуль. Для данной функции существует только один корень уравнения, но так бывает далеко не всегда.

Рассмотрим другой пример:

Подставим 0 в левую часть уравнения, как и в предыдущем примере:

Очевидно, что в данном случае нулей функции будет два: х=3 и х=-3. Если бы в уравнении был аргумент третьей степени, нулей было бы три. Можно сделать простой вывод, что количество корней многочлена соответствует максимальной степени агрумента в уравнении. Однако многие функции, например у=х 3 , на первый взгляд противоречат этому утверждению. Логика и здравый смысл подсказывают, что у этой функции только один нуль - в точке х=0. Но на самом деле корней три, просто все они совпадают. Если решать уравнение в комплексной форме, это становится очевидным. х=0 в данном случае, корень, кратность которого 3. В предыдущем примере нули не совпадали, потому имели кратность 1.

Алгоритм определения

Из представленных примеров видно, как определить нули функции. Алгоритм всегда один и тот же:

1. Записать функцию.
2. Подставить у или f(x)=0.
3. Решить получившееся уравнение.

Сложность последнего пункта зависит от степени аргумента уравнения. При решении уравнений высоких степеней особенно важно помнить, что количество корней уравнения равно максимальной степени аргумента. Особенно это актуально для тригонометрических уравнений, где деление обоих частей на синус или косинус приводит к потере корней.

Уравнения произвольной степени проще всего решать методом Горнера, который был разработан специально для нахождения нулей произвольного многочлена.

Значение нулей функций может быть как отрицательным, так и положительным, действительным или лежащим в комплексной плоскости, единичным или множественным. Или же корней уравнения может и не быть. Например, функция у=8 не приобретет нулевого значения ни при каком х, потому что она не зависит от этой переменной.

Уравнение у=х 2 -16 имеет два корня, и оба лежат в комплексной плоскости: х 1 =4і, х 2 =-4і.

Типичные ошибки

Частая ошибка, которую допускают школьники, еще не разобравшиеся толком в том, что такое нули функции, - это замена на ноль аргумента (х), а не значения (у) функции. Они уверенно подставляют в уравнение х=0 и, исходя из этого, находят у. Но это неправильный подход.

Другая ошибка, как уже упоминалось, сокращение на синус или косинус в тригонометрическом уравнении, из-за чего и теряется один или несколько нулей функции. Это не означает, что в таких уравнениях нельзя ничего сокращать, просто при дальнейших подсчетах необходимо учитывать эти "потерянные" сомножители.

Графическое представление

Понять, что такое нули функции, можно с помощью математических программ, таких как Maple. В ней можно построить график, указав желаемое количество точек и нужный масштаб. Те точки, в которых график пересечет ось ОХ, и есть искомые нули. Это один из самых быстрых способов нахождения корней многочлена, особенно если его порядок выше третьего. Так что если есть необходимость регулярно выполнять математические расчеты, находить корни многочленов произвольных степеней, строить графики, Maple или аналогичная программа будет просто незаменима для осуществления и проверки расчетов.

В котором она принимает нулевое значение. Например, для функции , заданной формулой

Является нулём, поскольку

Нули функции также называются корнями функции .

Понятие нулей функции можно рассматривать для любых функций, область значений которых содержит нуль или нулевой элемент соответствующей алгебраической структуры.

Для функции действительного переменного нулями являются значения, в которых график функции пересекает ось абсцисс .

Нахождение нулей функции часто требует использования численных методов (к примеру, метод Ньютона , градиентные методы).

Одной из нерешённых математических проблем является нахождение нулей дзета-функции Римана .

Корень многочлена

См. также

Литература

Wikimedia Foundation . 2010 .

Смотреть что такое "Нуль функции" в других словарях:

Точка, где заданная функция f (z) обращается в нуль; таким образом, Н. ф. f (z) это то же самое, что и корни уравнения f (z) = 0. Например, точки 0, π, π, 2π, 2π,... суть нули функции sinz. Нули аналитической функции (См. Аналитические… …

Нуль функция, нуль функции … Орфографический словарь-справочник

У этого термина существуют и другие значения, см. Нуль. Необходимо перенести содержимое этой статьи в статью «Нуль функции». Вы можете помочь проекту, объединив статьи. В случае необходимости обсуждения целесообразности объединения, замените этот … Википедия

Или C строка (от названия языка Си) или ASCIZ строка (от названия директивы ассемблера.asciz) способ представления строк в языках программирования, при котором вместо введения специального строкового типа используется массив символов, а концом… … Википедия

В квантовой теории поля принятое (жаргонное) название для свойства обращения в нуль фактора перенормировки константысвязи где g0 затравочная константа связи из лагранжиана взаимодействия, физ. константа связи, одетая взаимодействием. Равенство Z … Физическая энциклопедия

Нуль-мутация н-аллель - Нуль мутация, н. аллель * нуль мутацыя, н. алель * null mutation or n. allel or silent a. мутация, ведущая к полной потере функции в той последовательности ДНК, в которой она произошла … Генетика. Энциклопедический словарь

Утверждение в теории вероятностей о том, что всякое событие (т. н. остаточное событие), наступление к рого определяется лишь сколь угодно удаленными элементами последовательности независимых случайных событий или случайных величин, имеет… … Математическая энциклопедия

1) Число, обладающее тем свойством, что любое (действительное или комплексное) число при сложении с ним не меняется. Обозначается символом 0. Произведение любого числа на Н. равно Н.: Если произведение двух чисел равно Н., то один из сомножителей … Математическая энциклопедия

Функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции. Например, соотношение x2 + y2 1 = 0 задаёт Н. ф. … Большая советская энциклопедия